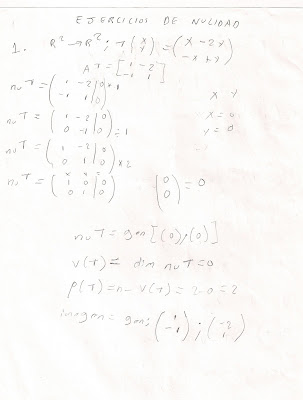
viernes, 27 de noviembre de 2009
viernes, 20 de noviembre de 2009
UNIDAD V Transformaciones Lineales
5.1.-Definición de transformación lineal y sus propiedades.
Transformación lineal.
Definición. Sean V y W espacios vectoriales. Una transformación lineal T de V en W es una función que asigna a cada vector v ∈ V un único vector Tv ∈ W y que satisface para cada u y v en V y cada escalar α,
T(u + v) = Tu + Tv (1)
T(αv) = αTv (2)
Notación. Escribimos T: V → W para indicar que T transforma V en W.
Terminología. Las transformaciones lineales se llaman, con frecuencia, operadores lineales. También, las funciones que satisfacen (1) y (2) se denominan funciones lineales.
Propiedades básicas de las transformaciones lineales.
Teorema 1. Sea T: V → W una transformación lineal. Entonces para todos los vectores u, v, v1, v2, ..., vn en V y todos los escalares α1, α2, ..., αn:
i. T(0) = 0
ii. T(u - v) = Tu - Tv
iii. T(α1v1, α2v2, ..., αnvn) = α1Tv1+ α2Tv2+ ... + αnTvn
Nota. En la parte (i) el 0 de la izquierda, es el vector cero en V mientras que el 0 del lado derecho, es el vector cero en W.
Teorema 2. Sea V un espacio vectorial de dimensión finita con base B={v1, v2, ..., vn}. Sean w1, w2, ..., wn n vectores en W. Suponga que T1 y T2 son dos transformaciones lineales de V en W tales que T1vi= T2vi = wi para i = 1, 2, ..., n.
Entonces para cualquier vector v ∈ V, T1v = T2v. Es decir T1 = T2.
Teorema 3. Sea V un espacio vectorial de dimensión finita con base B = {v1, v2, ..., vn}. Sea también W un espacio vectorial que contiene a los n vectores w1, w2, ..., wn. Entonces existe una única transformación lineal T: V → W tal que Tvi = wi para i = 1, 2, ..., n.
5.2.- Ejemplos de transformaciones lineales (reflexión, dilatación, contracción, rotación).
Rotación Sea 0 ≤ θ < v1 =" T" v2 =" T" u1 =" ū" u2 =" ū" v1 =" u1" v2 =" u2">
5.3.-Definición de núcleo o kernel, e imagen de una transformación lineal.
Transformación de Reflexión: La Transformación de T : R2 ―› R2 que a cada vector ū = (u1, u2) lo refleja sobre el eje x, para obtener un vector T (ū) = (v1, v2). En este caso, la situación es más sencilla ya que claramente tenemos dos triángulos rectángulos que son congruentes, de donde T queda definida como sigue: T (u1, u2) = (u1, -u2) Esta transformación se llama la reflexión sobre el eje x, y es lineal, ya que: T [(u1, u2) + γ(v1, v2)] = T (u1 + γv1, u2 + γv2) = (u1 + γv1, -u2 -γv2) = (u1, -u2) + γ(v1, -v2) = T (u1, u2) + γT (v1, v2) En este caso, la situación es más sencilla ya que claramente tenemos dos triángulos rectángulos que son congruentes, de donde T queda definida como sigue: T (u1, u2) = (u1, -u2) Esta transformación se llama la reflexión sobre el eje x, y es lineal, ya que: T [(u1, u2) + γ(v1, v2)] = T (u1 + γv1, u2 + γv2) = (u1 + γv1, -u2 -γv2) = (u1, -u2) + γ(v1, -v2) = T (u1, u2) + γT (v1, v2)
5.3.-Definición de núcleo o kernel, e imagen de una transformación lineal.
Kernel
Definición. Sean V y W espacios vectoriales y sea T : V → W una transformación lineal. Entonces:
El kernel (o núcleo) de T, denotado como ker T, está dado por
ker T = {v ∈ V: Tv = 0}
Obervación. Note que ker T es no vacío ya que por el Teorema 1 de las Transformaciones lineales, T(0) = 0 de manera que 0 ∈ ker T para toda transformación lineal T. Será interesante encontrar otros vectores en V que sean "mapeados al cero". De nuevo, nótese que cuando escribimos T(0) = 0, el 0 de la izquierda está en V, y el 0 de la derecha está en W.
Definición. Sean V y W espacios vectoriales y sea T : V → W una transformación lineal. Entonces:
El kernel (o núcleo) de T, denotado como ker T, está dado por
ker T = {v ∈ V: Tv = 0}
Obervación. Note que ker T es no vacío ya que por el Teorema 1 de las Transformaciones lineales, T(0) = 0 de manera que 0 ∈ ker T para toda transformación lineal T. Será interesante encontrar otros vectores en V que sean "mapeados al cero". De nuevo, nótese que cuando escribimos T(0) = 0, el 0 de la izquierda está en V, y el 0 de la derecha está en W.
Imagen de una transformación lineal.
Definición. Sean V y W espacios vectoriales y sea T : V → W una transformación lineal. Entonces:
imag V = { w ∈ W: w = Tv para alguna v ∈V}
Observación. El concepto imag T es simplemente el conjunto de "imágenes" de vectores en V bajo la transformación T. De hecho, si w = Tv, diremos que w es también la imagen de v bajo T.
Teorema. Si T : V → W es una transformación lineal, entonces:
i. ker T es un subespacio de V.
ii. imag T es un subespacio de W.
Demostración.
i. Sean u y v en ker T; entonces T(u + v) = Tu + Tv = 0 + 0 = 0 y T(αu) = αTu = α0 = 0 de modo que u + v y αu están en ker T.
ii. Sean w y x en imag T. Entonces w = Tu y x = Tv para dos vectores u y v en V. Esto significa que T(u + v) = Tu + Tv = w + x y T(αu) = αTu = αw. De esta manera w + x y αw están en imag T.
Ejemplo.
Sea Tv = 0 para todo v ∈ V. (T es la transformación cero.) Entonces ker T = V e imag T = {0}
imag V = { w ∈ W: w = Tv para alguna v ∈V}
Observación. El concepto imag T es simplemente el conjunto de "imágenes" de vectores en V bajo la transformación T. De hecho, si w = Tv, diremos que w es también la imagen de v bajo T.
Teorema. Si T : V → W es una transformación lineal, entonces:
i. ker T es un subespacio de V.
ii. imag T es un subespacio de W.
Demostración.
i. Sean u y v en ker T; entonces T(u + v) = Tu + Tv = 0 + 0 = 0 y T(αu) = αTu = α0 = 0 de modo que u + v y αu están en ker T.
ii. Sean w y x en imag T. Entonces w = Tu y x = Tv para dos vectores u y v en V. Esto significa que T(u + v) = Tu + Tv = w + x y T(αu) = αTu = αw. De esta manera w + x y αw están en imag T.
Ejemplo.
Sea Tv = 0 para todo v ∈ V. (T es la transformación cero.) Entonces ker T = V e imag T = {0}
viernes, 13 de noviembre de 2009
viernes, 30 de octubre de 2009
Espacios vectoriales: cambio de base
Espacios vectoriales: cambio de base
Muchas de las aplicaciones del álgebra lineal a la física, ingeniería, ciencias sociales, etc., pueden formularse de manera sencilla si se elige el sistema de coordenadas apropiado. También, los problemas de espacios vectoriales pueden simplificarse eligiendo una base adecuada. En la clase de hoy estudiaremos las coordenadas de un vector con respecto a una base fija, veremos que esas coordenadas cambian al cambiar la base del espacio y estudiaremos las relaciones que vinculan las coordenadas de un vector con respecto a diferentes bases.
Empezaremos con un ejemplo; tomemos B = { (1,0,-1), (-1,1,0), (1,1,1) } como base de Â3 y w = (2,-3,4) un vector en Â3. Expresaremos w como combinación lineal de B
-¿porqué esto es posible para cualquier w en Â3?.
Es decir, queremos encontrar escalares a, b, g tales que
(2,-3,4)=a(1,0,-1)+b(-1,1,0)+g(1,1,1)
lo cual nos lleva al sistema de ecuaciones,
a - b+g = 2
b+g =-3
-a +g = 4, cuya matriz aumentada es
-¿Son los escalares a, b, g únicos?
-¿Puede eliminar algún vector de B y todavía escribir w como combinación lineal de ese subconjunto?
En general tenemos el siguiente
Teorema 1:
Si (V,+,.) es un espacio vectorial de dimensión finita y B={v1, v2,...,vn} es una base de V, entonces para cada wÎV, existen escalares únicos a1, a2,...,an tales que w=a1v1+a2v2+...+anvn.
La existencia es debida a que una base es generadora del espacio y la unicidad es por el hecho de que la base es un conjunto linealmente independiente. En efecto, supongamos que w se puede escribir de dos maneras como una combinación lineal de v1, v2,...,vn; es decir,
w =a1v1+a2v2+...+anvn = b1v1+b2v2+...+bnvn, entonces,
(a1-b1)v1 + (a2-b2)v2 +...+ (an-bn)vn= 0 y como v1, v2,...,vn son l.i.
entonces a1 = b1, a2 = b2,..., an = bn.
Estos escalares únicos tienen un nombre propio: coordenadas de w con respecto a la base B. Precisando más, tenemos la siguiente
Definicion 1:
Sea como antes B={v1, v2,...,vn} una base de V y wÎV tal que w=a1v1+a2v2+...+anvn . Las coordenadas de w con respecto a la base B son a1, a2, ...,an y lo escribiremos así:
[w]B=( a1, a2,...,an).
Observaciones:
Ø si B={(1,2),(0,1)} entonces
[(2,7)]B= (2,3) porque (2,7)=2(1,2)+3(0,1)
Ø si C={(0,1),(1,2)} entonces
[(2,7)]C= (3,2) porque (2,7)=3(0,1)+ 2(1,2)
Es decir, [w]B no solo cambia cuando la base cambia, también depende del orden de los elementos en B. Por lo tanto, para definir con precisión las coordenadas de un vector w con respecto a una base B, pediremos que la base B sea una base ordenada.
Ejemplo 1:
Si S es la base canónica de Â3, como (2,-3,4) = 2(1,0,0)-3(0,1,0)+4(0,0,1) entonces [w]S=(2,-3,4) = w. Es decir, los vectores en Ân se denotan por sus coordenadas en la base canónica.
Los resultados obtenidos en el ejemplo anterior, nos permiten concluir que si w=(2,-3,4) y tomamos B={(1,0,-1),(-1,1,0),(1,1,1)} como base de Â3, entonces
Ejercicio Nº1:
Encuentre las coordenadas del polinomio
p(x)=1 +2x+3x2 con respecto a la base canónica de P2 , B={1, x, x2}.
Reflexione sobre el ejercicio.
¿Podríamos "ver" cada polinomio en P2 como si fuera vector en Â3? ¿Qué puede concluir?
Visualizar el cambio de base en Â2
(Para visualizar las coordenadas en las diferentes bases oprima el botón Av.Pag. de su teclado)
En la vida real ya hemos usado el concepto de coordenadas, por ejemplo al situar un punto de la tierra, por medio de su longitud y latitud (2 coordenadas) aunque es un punto en el espacio (tres coordenadas)
-¿Podría explicar esto en lenguaje de álgebra lineal?
Ahora estudiaremos cómo cambiar de una base B a otra C y encontraremos la matriz asociada a ese cambio de base.
Consideremos S, la base canónica en Â2 y B={u,v}={(1,1),(1,2)} otra base.
Sea w=(x,y) un vector en Â2 eso significa que w=x(1,0)+y(0,1). Como B es una base, queremos encontrar las coordenadas de w con respecto a esa base, es decir, encontrar a,b tales que w=au+bv=a(1,1)+b(1,2), lo que implicaría que [w]B=(a,b).
Además queremos explorar la relación entre (x,y) y (a,b).
Para encontrar (a,b), escribimos la base canónica como combinación lineal de la base B, es decir, (realice las cuentas)
(1,0) = 2(1,1)-1(1,2) y (0,1) = -1(1,1)+1(1,2),
sustituyendo en w = x(1,0)+y(0,1) Þ
w = x(1,0)+y(0,1) = x {2(1,1)-1(1,2)}+y{-1(1,1)+1(1,2)} Þ
w = (2x-y)(1,1)+ (-x+y)(1,2) = (2x-y)u + (-x+y)v Þ
a=2x-y y b=-x+y de dónde
, es decir
[w]B = [ [e1]B [e2]B ] * [w]S
La matriz es la matriz cambio de base de la base S a la base B porque esa es la acción que realiza.
En efecto [w]B=A[w]S
Definicion 2:
Sean B={u1, u2,...,un} y C={v1, v2,...,vn} bases de V. La matriz A cuyas columnas son [uj]C se llama matriz de transición o cambio de base de la base B a la base C y la denotaremos ABC=[(u1)C (u2)C ... (un)C]
Usando el mismo razonamiento que en el ejemplo anterior se puede probar
Teorema 2:
Sean B y C bases para el espacio vectorial V y sea A la matriz de transición de la base B a la base C, entonces para todo wÎV se satisface
(w)B=A(w)S
Ejercicio Nº2:
Sea S la base canónica en Â2 y B={(1,1),(-1,1)} otra base.
a) Encuentre A, la matriz de transición de la base S a la Base B
b) Encuentre P, la matriz de transición de la base B a la Base S
c) ¿Qué relación hay entre A y P?. Formule una conclusión y pruébela
d) Si [w]B=(3,-2), encuentre w
e) Si w=(3,-2), encuentre [w]B
Los resultados del ejercicio anterior, se satisfacen en general, es decir,
Teorema 3:
Sean B y C bases para el espacio vectorial V. Si A es la matriz de transición de la base B a la base C, entonces A-1 es la matriz de transición de la base C a la base B
Ejemplo 2:
Sea B={(1,0,-1),(-1,1,0),(1,1,1)} y
C ={(1,1,0),(1,0,1),(0,1,1)} bases de Â3.
Queremos hallar la matriz de transición de la base B a la Base C. Para ello expresamos los vectores de la base B como combinación lineal de los vectores de la base C, es decir
(1,0,-1) = a(1,1,0)+b(1,0,1)+g(0,1,1)
(-1,1,0) = a(1,1,0)+b(1,0,1)+g(0,1,1)
(1,1,1) = a(1,1,0)+b(1,0,1)+g(0,1,1), lo cual nos lleva a los 3 sistemas de ecuaciones que tienen la misma matriz,
1 = a+b
-1 = a+b
1 = a+b
0 = a+g
1 = a+g
1 = a+g
-1 = b+g
0 = b+g
1 = b+g
Û [(1,0,-1)]C = (1,0,-1) [(-1,1,0)]C = (0,-1,1) [(0,1,1)]C = (1/2,1/2,1/2)
por lo tanto la matriz de transición buscada es ,
en efecto, si w=(2,-3,4), en el ejemplo anterior comprobamos que
(2,-3,4)=-3(1,0,-1)-4(-1,1,0)+1(1,1,1) Þ
[(2,-3,4)]B=(-3,-4,1)
En efecto,
(-5/2)(1,1,0)+(9/2)(1,0,1)+(-1/2)(0,1,1)=(2,-3,4)
Ejercicio Nº3:
Sean B={4x-1,2x2-x,3x2+3}, C={1,1+x,1+x+x2)} bases de P2.
a) Encuentre A, la matriz de transición de la base B a la base C
b) Si [P(x)]B=(3,-2,1), encuentre [p(x)]C
c) Si [q(x)]C=(1,2,1),, encuentre [q(x)]B y q(x)
Solucion de los ejercicios
Solución1:
1+2x+3x2 = 1.1+2.x+3.x2 Þ [1+2x+3x2]B=(1,2,3)
Solución2:
a)
(1,0)=a(1,1)+b(-1,1) 1 , 0 =a-b
(0,1)=a(1,1)+b(-1,1) 0 , 1 =a+b
b)
(1,1) =a(1,0)+b(0,1) a= 1 b=1
(-1,1)=a(1,0)+b(0,1) a= -1 b=1
c)
Þ
A y P son matrices inversas
Conjetura: Si A es la matriz de transición de la base S a la base B, entonces A-1 es la matriz de transición de la base B a la base S,
En efecto, A[v]S = [v]B Þ [v]B = A-1[v]S
¿Porqué podemos asegurar que A es invertible?
d)
w=3(1,1)-2(-1,1) = (5,1)
e)
Solución3:
es la matriz de transición de la base B a la base canónica.
es la matriz de transición de la base C a la base canónica.
Por lo tanto Q-1 es la matriz de transición de la base canónica a la C.
Q-1P es la matriz de transición buscada; en efecto
Q-1*(P*[w]B)= Q-1*[w]S=[w]C
Muchas de las aplicaciones del álgebra lineal a la física, ingeniería, ciencias sociales, etc., pueden formularse de manera sencilla si se elige el sistema de coordenadas apropiado. También, los problemas de espacios vectoriales pueden simplificarse eligiendo una base adecuada. En la clase de hoy estudiaremos las coordenadas de un vector con respecto a una base fija, veremos que esas coordenadas cambian al cambiar la base del espacio y estudiaremos las relaciones que vinculan las coordenadas de un vector con respecto a diferentes bases.
Empezaremos con un ejemplo; tomemos B = { (1,0,-1), (-1,1,0), (1,1,1) } como base de Â3 y w = (2,-3,4) un vector en Â3. Expresaremos w como combinación lineal de B
-¿porqué esto es posible para cualquier w en Â3?.
Es decir, queremos encontrar escalares a, b, g tales que
(2,-3,4)=a(1,0,-1)+b(-1,1,0)+g(1,1,1)
lo cual nos lleva al sistema de ecuaciones,
a - b+g = 2
b+g =-3
-a +g = 4, cuya matriz aumentada es
-¿Son los escalares a, b, g únicos?
-¿Puede eliminar algún vector de B y todavía escribir w como combinación lineal de ese subconjunto?
En general tenemos el siguiente
Teorema 1:
Si (V,+,.) es un espacio vectorial de dimensión finita y B={v1, v2,...,vn} es una base de V, entonces para cada wÎV, existen escalares únicos a1, a2,...,an tales que w=a1v1+a2v2+...+anvn.
La existencia es debida a que una base es generadora del espacio y la unicidad es por el hecho de que la base es un conjunto linealmente independiente. En efecto, supongamos que w se puede escribir de dos maneras como una combinación lineal de v1, v2,...,vn; es decir,
w =a1v1+a2v2+...+anvn = b1v1+b2v2+...+bnvn, entonces,
(a1-b1)v1 + (a2-b2)v2 +...+ (an-bn)vn= 0 y como v1, v2,...,vn son l.i.
entonces a1 = b1, a2 = b2,..., an = bn.
Estos escalares únicos tienen un nombre propio: coordenadas de w con respecto a la base B. Precisando más, tenemos la siguiente
Definicion 1:
Sea como antes B={v1, v2,...,vn} una base de V y wÎV tal que w=a1v1+a2v2+...+anvn . Las coordenadas de w con respecto a la base B son a1, a2, ...,an y lo escribiremos así:
[w]B=( a1, a2,...,an).
Observaciones:
Ø si B={(1,2),(0,1)} entonces
[(2,7)]B= (2,3) porque (2,7)=2(1,2)+3(0,1)
Ø si C={(0,1),(1,2)} entonces
[(2,7)]C= (3,2) porque (2,7)=3(0,1)+ 2(1,2)
Es decir, [w]B no solo cambia cuando la base cambia, también depende del orden de los elementos en B. Por lo tanto, para definir con precisión las coordenadas de un vector w con respecto a una base B, pediremos que la base B sea una base ordenada.
Ejemplo 1:
Si S es la base canónica de Â3, como (2,-3,4) = 2(1,0,0)-3(0,1,0)+4(0,0,1) entonces [w]S=(2,-3,4) = w. Es decir, los vectores en Ân se denotan por sus coordenadas en la base canónica.
Los resultados obtenidos en el ejemplo anterior, nos permiten concluir que si w=(2,-3,4) y tomamos B={(1,0,-1),(-1,1,0),(1,1,1)} como base de Â3, entonces
Ejercicio Nº1:
Encuentre las coordenadas del polinomio
p(x)=1 +2x+3x2 con respecto a la base canónica de P2 , B={1, x, x2}.
Reflexione sobre el ejercicio.
¿Podríamos "ver" cada polinomio en P2 como si fuera vector en Â3? ¿Qué puede concluir?
Visualizar el cambio de base en Â2
(Para visualizar las coordenadas en las diferentes bases oprima el botón Av.Pag. de su teclado)
En la vida real ya hemos usado el concepto de coordenadas, por ejemplo al situar un punto de la tierra, por medio de su longitud y latitud (2 coordenadas) aunque es un punto en el espacio (tres coordenadas)
-¿Podría explicar esto en lenguaje de álgebra lineal?
Ahora estudiaremos cómo cambiar de una base B a otra C y encontraremos la matriz asociada a ese cambio de base.
Consideremos S, la base canónica en Â2 y B={u,v}={(1,1),(1,2)} otra base.
Sea w=(x,y) un vector en Â2 eso significa que w=x(1,0)+y(0,1). Como B es una base, queremos encontrar las coordenadas de w con respecto a esa base, es decir, encontrar a,b tales que w=au+bv=a(1,1)+b(1,2), lo que implicaría que [w]B=(a,b).
Además queremos explorar la relación entre (x,y) y (a,b).
Para encontrar (a,b), escribimos la base canónica como combinación lineal de la base B, es decir, (realice las cuentas)
(1,0) = 2(1,1)-1(1,2) y (0,1) = -1(1,1)+1(1,2),
sustituyendo en w = x(1,0)+y(0,1) Þ
w = x(1,0)+y(0,1) = x {2(1,1)-1(1,2)}+y{-1(1,1)+1(1,2)} Þ
w = (2x-y)(1,1)+ (-x+y)(1,2) = (2x-y)u + (-x+y)v Þ
a=2x-y y b=-x+y de dónde
, es decir
[w]B = [ [e1]B [e2]B ] * [w]S
La matriz es la matriz cambio de base de la base S a la base B porque esa es la acción que realiza.
En efecto [w]B=A[w]S
Definicion 2:
Sean B={u1, u2,...,un} y C={v1, v2,...,vn} bases de V. La matriz A cuyas columnas son [uj]C se llama matriz de transición o cambio de base de la base B a la base C y la denotaremos ABC=[(u1)C (u2)C ... (un)C]
Usando el mismo razonamiento que en el ejemplo anterior se puede probar
Teorema 2:
Sean B y C bases para el espacio vectorial V y sea A la matriz de transición de la base B a la base C, entonces para todo wÎV se satisface
(w)B=A(w)S
Ejercicio Nº2:
Sea S la base canónica en Â2 y B={(1,1),(-1,1)} otra base.
a) Encuentre A, la matriz de transición de la base S a la Base B
b) Encuentre P, la matriz de transición de la base B a la Base S
c) ¿Qué relación hay entre A y P?. Formule una conclusión y pruébela
d) Si [w]B=(3,-2), encuentre w
e) Si w=(3,-2), encuentre [w]B
Los resultados del ejercicio anterior, se satisfacen en general, es decir,
Teorema 3:
Sean B y C bases para el espacio vectorial V. Si A es la matriz de transición de la base B a la base C, entonces A-1 es la matriz de transición de la base C a la base B
Ejemplo 2:
Sea B={(1,0,-1),(-1,1,0),(1,1,1)} y
C ={(1,1,0),(1,0,1),(0,1,1)} bases de Â3.
Queremos hallar la matriz de transición de la base B a la Base C. Para ello expresamos los vectores de la base B como combinación lineal de los vectores de la base C, es decir
(1,0,-1) = a(1,1,0)+b(1,0,1)+g(0,1,1)
(-1,1,0) = a(1,1,0)+b(1,0,1)+g(0,1,1)
(1,1,1) = a(1,1,0)+b(1,0,1)+g(0,1,1), lo cual nos lleva a los 3 sistemas de ecuaciones que tienen la misma matriz,
1 = a+b
-1 = a+b
1 = a+b
0 = a+g
1 = a+g
1 = a+g
-1 = b+g
0 = b+g
1 = b+g
Û [(1,0,-1)]C = (1,0,-1) [(-1,1,0)]C = (0,-1,1) [(0,1,1)]C = (1/2,1/2,1/2)
por lo tanto la matriz de transición buscada es ,
en efecto, si w=(2,-3,4), en el ejemplo anterior comprobamos que
(2,-3,4)=-3(1,0,-1)-4(-1,1,0)+1(1,1,1) Þ
[(2,-3,4)]B=(-3,-4,1)
En efecto,
(-5/2)(1,1,0)+(9/2)(1,0,1)+(-1/2)(0,1,1)=(2,-3,4)
Ejercicio Nº3:
Sean B={4x-1,2x2-x,3x2+3}, C={1,1+x,1+x+x2)} bases de P2.
a) Encuentre A, la matriz de transición de la base B a la base C
b) Si [P(x)]B=(3,-2,1), encuentre [p(x)]C
c) Si [q(x)]C=(1,2,1),, encuentre [q(x)]B y q(x)
Solucion de los ejercicios
Solución1:
1+2x+3x2 = 1.1+2.x+3.x2 Þ [1+2x+3x2]B=(1,2,3)
Solución2:
a)
(1,0)=a(1,1)+b(-1,1) 1 , 0 =a-b
(0,1)=a(1,1)+b(-1,1) 0 , 1 =a+b
b)
(1,1) =a(1,0)+b(0,1) a= 1 b=1
(-1,1)=a(1,0)+b(0,1) a= -1 b=1
c)
Þ
A y P son matrices inversas
Conjetura: Si A es la matriz de transición de la base S a la base B, entonces A-1 es la matriz de transición de la base B a la base S,
En efecto, A[v]S = [v]B Þ [v]B = A-1[v]S
¿Porqué podemos asegurar que A es invertible?
d)
w=3(1,1)-2(-1,1) = (5,1)
e)
Solución3:
es la matriz de transición de la base B a la base canónica.
es la matriz de transición de la base C a la base canónica.
Por lo tanto Q-1 es la matriz de transición de la base canónica a la C.
Q-1P es la matriz de transición buscada; en efecto
Q-1*(P*[w]B)= Q-1*[w]S=[w]C
Dimensión de un espacio vectorial
Dimensión de un espacio vectorial
Un espacio vectorial sobre un cuerpo que se dice que tiene dimensión si existe una base de cardinal n. En un espacio vectorial, todas las bases tienen el mismo cardinal, lo que hace de la dimensión el primer invariante del álgebra lineal. El espacio vectorial trivial {0} tiene como dimensión 0 porque el conjunto vacío es su base: una combinación de cero vector da el vector nulo.
Intuitivamente hablando, la dimensión de un espacio vectorial nos dice cuántos elementos necesitamos para poder expresar cualquier elemento del espacio en términos de las combinaciones lineales de los primeros, i.e., cuántos elementos del espacio necesitamos para poder expresar todos los elementos del espacio como sumas de múltiplos de éstos elementos.
Un espacio vectorial sobre un cuerpo que se dice que tiene dimensión si existe una base de cardinal n. En un espacio vectorial, todas las bases tienen el mismo cardinal, lo que hace de la dimensión el primer invariante del álgebra lineal. El espacio vectorial trivial {0} tiene como dimensión 0 porque el conjunto vacío es su base: una combinación de cero vector da el vector nulo.
Intuitivamente hablando, la dimensión de un espacio vectorial nos dice cuántos elementos necesitamos para poder expresar cualquier elemento del espacio en términos de las combinaciones lineales de los primeros, i.e., cuántos elementos del espacio necesitamos para poder expresar todos los elementos del espacio como sumas de múltiplos de éstos elementos.
viernes, 23 de octubre de 2009
viernes, 9 de octubre de 2009
lunes, 5 de octubre de 2009
Suscribirse a:
Comentarios (Atom)
















































